CSDataStructure

[자료구조] 트리(Tree)

CS, DataStructure

트리(Tree)

리스트와 스택, 큐는 자료들의 선의 형태로 나열되어 있는 구조를 가진 선형 자료구조였다. 자료들이 나열도니 구조가 선형이 아닌 자료구조를 비선형 자료구조라고 하는데, 트리(Tree)는 비선형 자료구조 중에서 자료들 간에 계층관계를 가진 계층형 자료구조이다.

  • 트리는 정점(Node, 노드)과 선분(Branch, 가지)을 이용하여 사이클을 이루지 않도록 구성한 Graph의 특수한 형태이다.
  • 가족의 계보(족보), 연산 수식, 회사 조직 구조도, 히프(Heap) 등을 표현하기에 적합하다.

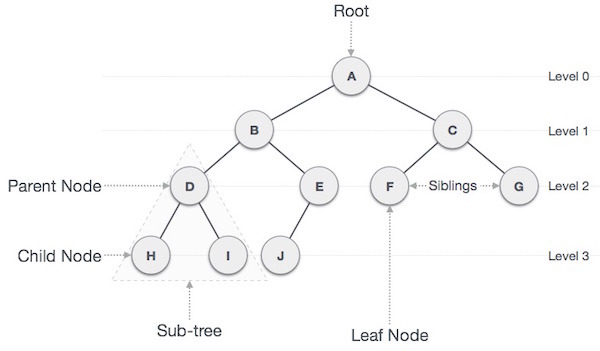
트리 관련 용어

  • 노드(Node) : 트리의 기본 요소로서 자료 항목과 다른 항목에 대한 가지(Branch)를 합친 것
  • 근 노드(Root Node) : 트리의 맨 위에 있는 노드
  • 디그리(Degree, 차수) : 각 노드에서 아래로 뻗어나온 가지의 수
  • 단말 노드(Terminal Node) = 잎 노드(Leaf Node) : 자식이 하나도 없는 노드, Degree가 0인 노드
  • 비단말 노드(Non-Terminal Node) : 자식이 하나라도 있는 노드, 즉 Degree가 0이 아닌 노드
  • 조상 노드(Ancestors Node) : 임의의 노드에서 근 노드에 이르는 경로상에 있는 노드들
  • 자식 노드(Child Node) : 어떤 노드에 연결된 다음 레벨의 노드들
  • 부모 노드(Parent Node) : 어떤 노드에 연결된 이전 레벨의 노드들
  • 형제 노드(Brother Node, Sibling) : 동일한 부모를 갖는 노드들
  • Level : 근 노드의 Level을 1로 가정한 후 어떤 Level이 L이면 자식 노드는 L+1
  • 깊이(Depth, Height) : Tree에서 노드가 가질 수 있는 최대의 레벨
  • 숲(Forest) : 여러 개의 트리가 모여 있는 것
  • 트리의 디그리 : 노드들의 디그리 중에서 가장 많은 수


이진 트리

트리의 노드 구조를 일정하게 정의하면 트리의 연산이 단순화되어 쉬워진다. 그래서 모든 노드의 차수를 2 이하로 정하여 전체 트리의 차수가 2 이하가 되도록 만든 것이 이진 트리(Binary Tree)다.

이진 트리는 왼쪽 자식 노드와 오른쪽 자식 노드 2개만을 가질 수 있다. 이진 트리에 있는 모든 노드는 왼쪽 자식 노드를 루트로 하는 왼쪽 서브 트리와 오른쪽 자식 노드를 루트로 하는 오른쪽 서브 트리를 가진다. 그리고 이진 트리의 서브 트리들 역시 모두 이진 트리여야 한다.

이진 트리의 종류로 포화 이진 트리, 완전 이진 트리, 편향 이진 트리가 있다.


포화 이진 트리(Full Binary Tree)

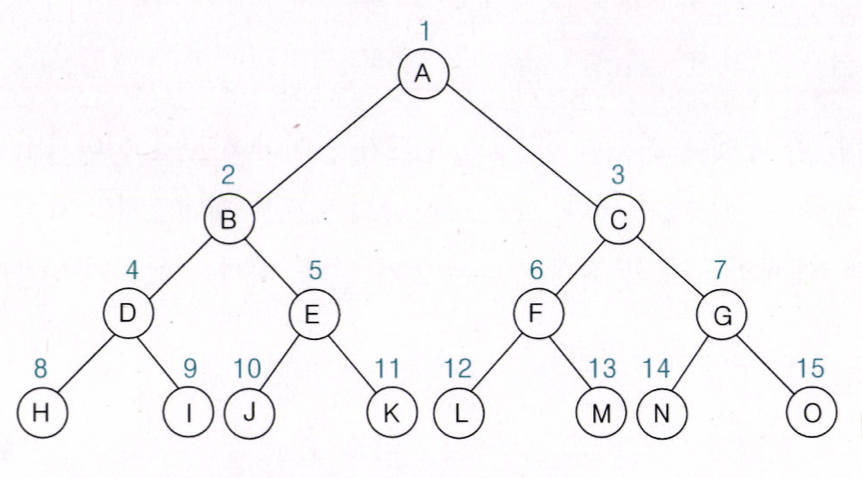
포화 이진 트리는 모든 레벨에 노드가 꽉 차서 포화 상태인 이진 트리를 의미한다. 즉 포화 이진 트리는 높이가 h일 때 2h+1-1개의 최대 노드 수를 갖는 이진 트리다. 포화 이진 트리의 노드는 위치에 따라 일정한 노드 번호를 붙일 수 있다. 루트 노드를 1번으로 하고, 레벨 별로 왼쪽에서 오른쪽으로 차례로 2h+1-1까지 번호를 붙일 수 있다.


완전 이진 트리(Complete Binary Tree)

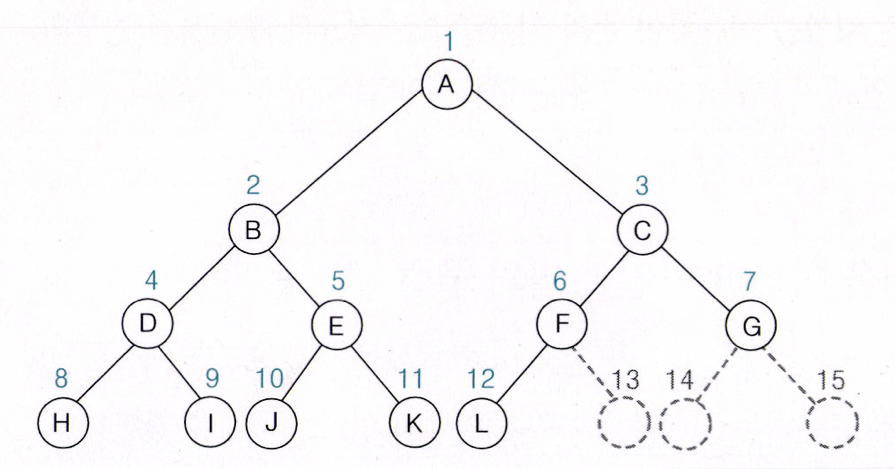
완전 이진 트리는 높이가 h이고 노드 수가 n개일 때, 노드의 위치가 포화 이진 트리의 노드 1번부터 n번까지의 위치와 완전히 일치하는 이진 트리다. 따라서 이진 트리에서는 n+1번부터 2h+1-1번까지의 노드는 공백 노드가 된다.


편향 이진 트리(Skewed Binary Tree)

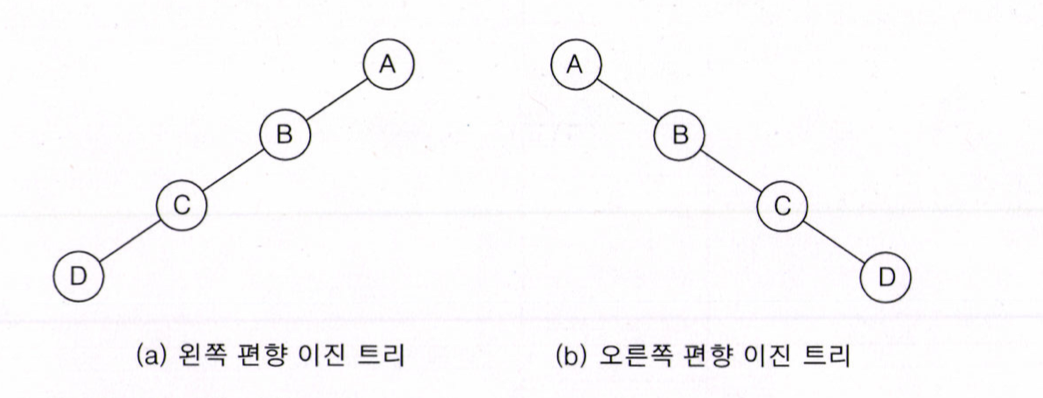
이진 트리 중에서 최소 개수의 노드를 가지면서 왼쪽이나 오른쪽 서브 트리만 가지고 있는 트리를 편향 이진트리라고 한다.

Share